Yhdeksänmenetelmä peruslaskutoimitusten (kerto-, yhteen- ja vähennyslasku) tarkistamisessa

Lue artikkeli kokonaisuudessaan pdf:nä verkkolehdestä >

Kertolasku

Et ole varmaankaan koskaan halunnut tarkistaa, onko laskutoimitus 1234∙5678=7005652 oikein laskettu? Silloin tämä artikkeli ei ole Sinua varten. Älä missään nimessä kiusaa itseäsi lukemalla artikkelia pidemmälle.

Kiusasit itseäsi lukemalla artikkelia ainakin tähän kappaleeseen saakka. Jatka siis loppuun saakka. Moni sortuu tarkistamaan laskun laskimella. Et kai juuri äsken tuottanut pettymystä itsellesi tekemällä samoin? Usko hyvällä. Laita se laskin jo pois. Ja ei. Kännykän laskintakaan ei saa käyttää.

Laskutoimitus voidaan tarkistaa yllättävän helposti ns. 9-menetelmällä. Tämä on aika monelle vieras menetelmä, mutta se on erittäin kätevä tapa tarkistaa laskutoimituksia.

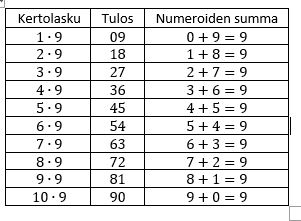
Idea perustuu loppujen lopuksi yksinkertaiseen havaintoon, jonka moni on varmasti tehnyt jo ala-asteella opetellessaan luvun 9 kertotaulua. Kertolaskujen 1∙9, 2∙9, …, 10∙9 lopputulokset saa mekaanisesti aikaiseksi kirjoittamalla ensin allekkain numerot 0…9 (eli kasvavaan järjestykseen) ja sen jälkeen niiden rinnalle numerot 9…0 (eli laskevaan järjestykseen). Tällöin saadaan aikaiseksi taulukko 1. Taulukon kolmannessa sarakkeessa todetaan, että kun lukua 9 kerrotaan kokonaisluvulla 1…10, niin saadaan aina aikaiseksi luku, jonka muodostamien numeroiden summa eli ns. poikkisumma on 9.

Taulukko 1. Yhdeksän kertotaulu, kun kertojana on luku väliltä 1…10

Entä sitten tästä eteenpäin? Katsotaan yhdeksän kertotaulua pidemmälle. Taulukon 2 kolmas sarake on kovin ns. yhdeksänvoittoinen. Ainoastaan ensimmäinen luku on yhdeksästä poikkeava, mutta sekin on 18 eli jos tämän luvun numerot lasketaan yhteen 1+8, niin päädytään jälleen poikkisumman arvoon 9.

Taulukko 2. Yhdeksän kertotaulu, kun kertojana on luku väliltä 11…20

Ei ryhdytä tässä vaiheessa sen tarkemmin asiaa perustelemaan, mutta luvulla 9 jaolliset luvut ovat todellakin kaikki sellaisia, että niiden numeroiden poikkisummaksi joko suoraan tai useampien summausvaiheiden kautta saadaan aina 9.

Jos tutkitaan vaikkapa lukua 67982342454, niin numerot yhteen laskemalla saadaan summaksi 6+7+9+8+2+3+4+2+4+5+4=54, jonka numerot jälleen yhteen laskemalla antavat 5+4=9. Näin ollen tiedetään, että luku 67982342454 on jaollinen 9:llä. Laskimella voi itse kukin tarkistaa, että 67982342454/9 antaa vastaukseksi kokonaisluvun 7553593606.

”Eikö tämä ole ihan kertakaikkisen joutavaa filosofiaa? Mitä hyötyä tästä on? Miksi ihmeessä edes luen tätä artikkelia?”, ajattelet varmaankin?

Tuska lisää tietoa, joten jatketaan pohdiskelua. Olemme tähän asti keskittyneet vain yhdeksällä jaollisiin lukuihin. Suurin osa luvuista ei ole yhdeksällä jaollisia. Itse asiassa vain joka yhdeksäs kokonaisluku on jaollinen yhdeksällä. Tutkitaanpa, mitä tapahtuu, kun jaetaan mielivaltainen luku 9:llä. Olkoon tämä mielivaltainen luku vaikkapa 193. Koska pidän itsestäni ja ennen kaikkea omasta käsialastani, lasken lukijoiden riemuksi jakokulmassa jakolaskun 193/9. Tätä voidaan ihastella kuvassa 1.

Jos muistaa vielä jakokulmassa laskemisen periaatteen, voi kuvan perusteella päätellä, että  193/9 = 21 4/9 eli siis jakojäännökseksi tuli luku 4.

Tutkitaanpa edelleen lukua 193 . Lasketaan numerot yhteen.  1 + 9 +3 =13 ja jatketaan yhteenlaskua vielä saadun summan osalta 1+3 =4 . Saatiin siis sama luku kuin jakojäännös 9:llä jaettaessa. Onko tämä sattumaa?

Tämä ei ole sattumaa. Tämä on Satumaa, sillä toisin kuin saduissa, näin käy joka kerta mutta myös aina. Vakuutut varmasti asiasta, kun repäisemme hatusta sattumanvaraisen luvun 564589  ja laskemme summan 5+6+4+5+8+9=37 ja jatkamme nauraen laskemalla  3+7=10 ja toteamalla hämmentyneenä, että 1+0 =1 eli jakojäännökseksi tulisi muka 1. Tämä kuulostaa uskottavalta, sillä laskin kertoo, että 564589/9=62732.1111…  ja tämä päättymätön ykkösistä koostuva desimaaliosahan on tuttu luku 1/9 eli jakojäännös tosiaan on 1.

Jakojäännöksen voi laskea nopeamminkin ”unohtamalla hallitusti” summasta luvut 9 eli luvulla 564589  voidaan laskea vain 5+6+4+5+8 =28  ja siitä edelleen 2+8=1+  ja vielä 1+0=1 .

Rutinoituneet jakojäännösten metsästäjät oppivat myös ”unohtamaan vielä hallitummin” summasta kaikki sellaiset numerot, joiden summaksi tulee 9 tai joku muu yhdeksällä jaollinen luku. Eli siis luvulla 564589 voidaan viimeisen numeron 9 lisäksi jättää keskellä olevat 4 ja 5 pois ja laskea vain 5+6+8=19 ja edelleen 1+9=1+  ja lopulta 1+0=1 .

Mennään sitten lopulta takaisin alussa esittämäämme ongelmaan.  Artikkeli jatkuu. Helppolukuisuuden ja kaavojen vuoksi @SeAMKin toimituskunta on tallentanut artikkelin kokonaisuudessaan pdf:ksi. Lue koko artikkeli täältä.

Juhani Paananen, lehtori, SeAMK Tekniikka