Laskuviivaimella laskeminen - peruslaskutoimitukset

Lapsena ihmettelin usein isäni kirjoituspöydän laatikosta löytynyttä merkillistä ”viivoitinta”. Tässä viivoittimessa (Kuva 1) oli useita erilaisia lukuasteikkoja ja kaiken lisäksi keskellä viivoitinta oli liikkuva osa nimeltään ”kieli” ja koko tikun päällä outo läpinäkyvä muovilevy nimeltään ”juoksija”. Myöhemmin minulle selvisi, että kyseessä ei ollut mikään pelkkä viivoitin vaan sehän oli oikeastaan eräs ihmiskunnan suurimpia keksintöjä kautta aikain. Isäni kirjoituspöytä kätki sisäänsä laskuviivaimen eli laskutikun.

Kuva 1. Laskuviivain A.W. Faber – Castell 57/87 Rietz Schul – Rechenstab

Vaikka myöhemmin elämässäni ajauduin valitettavasti huonoon seuraan ja vajosin matemaattisten aineiden opettajaksi, en koskaan vaivautunut opettelemaan laskuviivaimen käyttöä. Vasta viime vuosina olen hankkinut osaamista tämän ihmeellisen teknisen laskentavälineen käytöstä ja aikomukseni on nyt tätä tietämystäni jakaa innostuneille mutta kiinnostuneille lukijoilleni.

Käyn tässä artikkelissani läpi yksinkertaisia peruslaskutoimituksia, joiden laskemisessa laskuviivain on aikanaan suorastaan mullistanut maailman. Käytän jatkossa nimitystä ”laskutikku” lähinnä siksi, koska kyseinen nimi oli aikanaan puhekielessä käytössä ja on myös itselleni tutumpi kuin ehkä hieman asiallisemman kuuloinen ”laskuviivain”.

Kertolasku

Oletetaan, että halutaan laskea laskutikun avulla kertolasku 2·3. Jokainen toki tietää vastauksen jo ilman laskutikkuakin, mutta katsotaan periaate aluksi. Siirretään aluksi laskutikun kieli asentoon, jossa kielen C-asteikon vasemman pään alkupiste (jossa on lukema 1) asettuu laskutikun D-asteikon kohtaan 2. Tämä näkyy kuvassa 2.   Tämän jälkeen haetaan C-asteikolta luku 3 ja luetaan sen alapuolelta D-asteikolta vastaus 6. Helppoa, eikö vaan?

Itse asiassa, kun kieli on asetettu 2:n kohdalle, voidaan laskutikusta lukea samalla lukuisia muitakin kahdella kertomisia. Kuvasta nähdään esimerkiksi, että 2·1,5=3 ja 2·2=4.

Kuva 2. Kertolasku 2·3  laskutikun avulla

Videolinkki (kertolasku  laskutikun avulla): https://youtu.be/rZ8A1pMfROU

Entä sitten, jos pitäisi laskea monimutkaisempi laskutoimitus, esimerkiksi 2,23·1,58? Homma onnistuu aivan vastaavalla tavalla, joskin nyt joudutaan jo jonkin verran tekemisiin arviointikyvyn kanssa. Ilmeisestikin on niin, että kokenut laskutikun käyttäjä kykenee arvioimaan laskutikun asteikkoja huomattavasti tarkemmin kuin mihin itse pystyn, mutta melko hyviin tuloksiin vaatimattomallakin kokemuksella pääsee.

Asetetaan kielen C-asteikon vasen alkupiste D-asteikon lukeman  2,23 kohdalle. Tämä on esitettynä kuvassa 3. Sen jälkeen siirretään juoksijaa siten, että sen keskellä oleva pystysuora hiusviiva asettuu C-asteikon lukeman 1,58  kohdalle. Tämän jälkeen arvioidaan D-asteikolta vastaus. Tällä kohdalla D-asteikon viivoitukset ovat 0.02 yksikön tarkkuudella. Vastaus on laskutikun perusteella välillä 3,52…3,54 . Tarkempi arvioni on 3.524.  Kun nykyaikaisen laskimen avulla katsoin oikean vastauksen, oli se 3.5234 eli laskutikun avulla saamani tuloksen suhteellinen virhe oli noin 0.02 %.

Kuva 3. Kertolasku  laskutikun avulla

Videolinkki (kertolasku  laskutikun avulla): https://youtu.be/mXifUxtj5gU

Laskutikun C- ja D-asteikot käsittävät molemmat lukuvälin 1..10. Entä, jos pitäisi laskea vaikkapa 52,4·78,6  ? Heittivätkö entisajan insinöörit, merkonomit ynnä reippaat pojat sekä tytöt silloin laskutikun nurkkaan ja tyytyivät katkeroituneina käyttämään tietokonetta tai taskulaskinta? Eivät tietenkään. Hetkisen itkeskelyn jälkeen he muistivat, ettei tietokoneita tai taskulaskimia ollut olemassakaan tai ainakaan heidän varoillaan hankittavissa. Samalla he hoksasivat, että lasku lasketaan laskutikulla aivan samoin kuin pienemmilläkin luvuilla. Täytyy vain aluksi unohtaa pilkkujen paikat ja lukujen suuruusluokat ja laskea lasku vastaavasti kuin aiemmissa esimerkeissä. Lopuksi vain päätellään vastauksen suuruusluokka ja tätä kautta pilkun paikka.

Eli siirretään aluksi kieli keskelle suuta ja samalla vaivalla laskutikun kielen C-asteikon alkupää kohtaan 524. Tämä näkyy kuvasta 4. Saman kuvan avulla voi treenata omaa pettymyksensietokykyään. Kun nimittäin siirtää katsettaan laskutikun kielen C-asteikkoa oikealle päin, havaitsee ettei kuvassa näy tarvittavaa lukemaa 786 lainkaan. Kieli on nyt sellaisessa asennossa, ettei vastausta ole mahdollista lukea samaan tapaan D-asteikolta kuten aiemmin.

Kuva 4. Kertolasku 52,4·78,6 laskutikun avulla. Siitä ei tule mitään tällä menetelmällä.

Me laskutikun ystävät emme kuitenkaan anna moisen vastoinkäymisen ajaa mielialaamme matalasuhdanteeseen. Jos ei homma toimi perinteiseen tyyliin asettamalla kielen C-asteikon alkupää D-asteikon lukeman 524 kohdalle, niin tehdään asia toisinpäin. Eli siirretäänkin C-asteikon loppupää tämän lukeman kohdalle. Kielen oikeassa päässä asteikon nimenä on tosin X, mutta emme anna tämän itseämme kohtuuttomasti hämätä.

Juoksijan hiusviiva asetetaan seuraavaksi kielen asteikon kohtaan 786 ja luetaan D-asteikolta lukema 412. Tässä vaiheessa muistetaan, että olemme laskussa unohtaneet desimaalipilkut. Oikea vastaus on siis suunnilleen luvun 412 jokin kymmenmonikerta tai jokin kymmenesosista. Siis oikea vastaus voi olla esimerkiksi 4.12 tai 41.2 tai 412 tai 4120 tai 41200 tai 412000 tai mikä tahansa muukin vastaava kymmenen kerrannainen.

Kuva 5. Kertolasku 52,4·78,6 laskutikun avulla. Siitä saadaan tulos tällä kertaa.

Nyt palautellaan mieliin alkuperäinen lasku. Sehän oli 52,4·78,6 . Lasketaan kertolaskulle alalikiarvo ja ylälikiarvo. Tiedetään, että oikea vastaus on luku, jonka täytyy olla suurempi kuin 50·70=3500  ja pienempi kuin 60·80=4800. Edellisestä luettelosta hyväksytään siis vaihtoehto 4120, joka ainoana osuu tälle oikean vastauksen sallitulle vaihteluvälille.

Laskimen perusteella tarkka vastaus olisi ollut 52,4·78,6=4118.64 . Koska laskinta ei luonnollisesti ollut käytössä aikana, jolloin laskimen käyttö olisi ollut luonnotonta, jouduin alati hiipuvan uskottavuuteni vuoksi tarkistamaan laskun allekkain kertolaskulla. Osasin sen enää töin tuskin, mikä häpeäkseni todettakoon vaan ei anteeksi annettakoon. Tulokseksi sain kuitenkin saman kuin laskimella ja likimain saman kuin laskutikulla, mitä tulosta nyt ei suinkaan tarvitse sentään hävetä. Tuloksen suhteellinen virhe oli 0.03 %, mikä on vähintäänkin kohtuullinen.

Kuva 6. Kertolasku  allekkain kertolaskun avulla.

Videolinkki (kertolasku  laskutikun avulla): https://youtu.be/pDL4Y5wQKh8

Jakolasku

Lähdetään jälleen liikkeelle helposta esimerkistä. Oletetaan, että halutaan laskea jakolasku 5/2 . Siirretään aluksi laskutikun kieli asentoon, jossa kielen C-asteikon lukema 5 asettuu täsmälleen D-asteikon lukeman 2 yläpuolelle. Tämä on melko loogista, eli osoittaja on nimittäjän yläpuolella. Sen jälkeen luetaan vastaus kielen C-asteikolta kohdasta, joka osuu D-asteikon alkupäähän. Tulokseksi saadaan 2.5, joka on aivan oikea vastaus.

Kuva 7. Jakolasku  laskutikun avulla.

Tässä vaiheessa kannattaa pysähtyä hetkeksi. Kun suoritettiin lukujen 5 ja 2 jakolaskua, niin vasemmassa päässä rungon D-asteikon alkupiste asettui kielen C-asteikon lukeman 2.5 kohdalle. Mitä tapahtui samaan aikaan laskutikun oikeassa päässä? Tämä ilmenee kuvasta 8. Havaitaan, että kielen C-asteikon loppupiste (eli lukema 10) asettui rungon C-asteikon lukeman 4 kohdalle. Tämä tarkoittaa, että jakolaskun suorittaminen toisinpäin antaa tulokseksi luvun, joka on luvun 4 kymmenesosa eli siis 0.4.

Eli mitä opimme? Kun asetetaan kielen lukema 5 ja rungon lukema 2 päällekkäin, saadaan laskutikun vasemmasta päästä laskutoimituksen 5/2  tulos 2.5 ja oikeasta päästä laskutoimituksen 2/5  tulos  eli 0.4. Periaate on se, että vasemmalta puolelta luetaan aina sen jakolaskun lopputulos, jossa osoittaja on nimittäjää suurempi.

Kuva 8. Jakolasku  laskutikun avulla.

Videolinkki (jakolasku  laskutikun avulla): https://youtu.be/OCRzvrajKZE

Seuraavaksi haemmekin haasteita oikein kunnolla eli yritämme laskea laskutoimituksen

laskutikulla. Haemme aluksi nimittäjän 3.11763 laskutikun D-asteikolta. Tarkasti emme sitä lukua löydä, sillä asteikon tuolla alueella viivoitukset ovat 0.02 yksikön välein. Lukema 3.12 on kuitenkin helppo löytää ja on jopa mahdollista arvioida lukeman 3.11763 paikkaa likimain. Kokemus parantaa arviointitarkkuutta merkittävästi. Juoksijan hiusviiva asetetaan tähän arvioituun kohtaan.

Osoittajasta toteamme saman tien, että lukemaa 12.84678 emme laskutikun asteikolta löydä, koska asteikon lukemat ovat vain väliltä 1…10. Se ei kumminkaan haittaa, sillä emme piittaa tässä vaiheessa pilkun oikeasta paikasta. Haemme sen sijaan kielen C-asteikolta lukemaa 1.284678. Tätäkään emme tarkasti sieltä löydä, mutta C-asteikon tällä alueella viivoitukset ovat 0.01 yksikön välein ja esimerkiksi lukema 1.285 on varsin tarkasti löydettävissä. Siirretään kieli asentoon, jossa nämä laskutoimituksen osoittaja ja nimittäjä ovat molemmat hiusviivan kohdalla.

Kun tulosta luetaan, täytyy huomioida, että laskutikulla suoritamme itse asiassa laskutoimituksen  sijasta laskutoimitusta 1.284678/3.11763

eli osoittaja on nimittäjää pienempi. Tällöin vastaus luetaan laskutikun oikeasta päästä ja siellä arviolta likimain 412 (tai jokin tämän kymmenmonikerta).

Kuva 9. Jakolasku  laskutikun avulla.

Seuraavaksi päätellään lopputuloksen pilkun paikka. Laskutoimituksen  alalikiarvo on  12/4=3 ja ylälikiarvo 13/3=4 1/3 . Voidaan näin ollen päätellä, että ≈4.12

Laskimella saatu tarkka vastaus on  =4.1206… eli laskutikun avulla saatuun tulosarvioon sisältyy tällä kertaa likimain 0.02 % suhteellinen virhe.

Videolinkki (jakolasku   laskutikun avulla): https://youtu.be/cwtU26bEx1A

Toiseen potenssiin korottaminen ja neliöjuuri

Kun laskutikun avulla suoritetaan toiseen potenssiin korotus tai otetaan neliöjuuri, voidaan laskutikun kieli poistaa tarpeettomana ja käyttää laskennassa pelkkää runkoa.

Jos esimerkiksi täytyy laskea 3.53² , niin asetetaan juoksijan hiusviiva X-asteikon (sama asteikko kuin D-asteikko) lukemaan 3.53 ja luetaan vastaus X²-asteikolta. Tulos on arviolta 12.45. Laskimen avulla saatu tarkka vastaus on 12.4609 eli suhteellinen virhe on likimain 0.09 %.

Kuva 10. Laskutoimitus  laskutikun avulla.

Videolinkki (laskutoimitus  laskutikun avulla): https://youtu.be/egLfvundNRI

Neliöjuuri saadaan seuraavasti. Jos halutaan saada esimerkiksi luvun 15678 neliöjuuri, niin aluksi juurrettavaa lukua jaetaan sadalla niin kauan, kunnes saadaan se muunnettua luvuksi, joka on välillä 1…100. Nyt siis

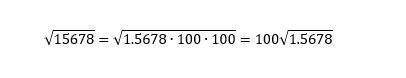
Asetetaan juoksijan hiusviiva X²-asteikon lukemaa 1.5678  vastaavalle kohdalle ja luetaan vastaus X-asteikolta. Tulos on likimain 1.252 eli siis

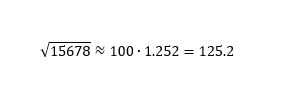
Laskimen avulla saatu tarkka vastaus on

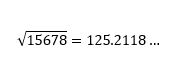
eli suhteellinen virhe on likimain 0.01 %.

Kuva 11. Luvun  neliöjuuri laskutikun avulla.

Videolinkki (neliöjuuri  laskutikun avulla): https://youtu.be/nRh37Dqvwf4

Kolmanteen potenssiin korottaminen ja kuutiojuuri

Luvun kolmas potenssi ja kuutiojuuri saadaan helpoimmin, kun käytetään laskennassa pelkkää runkoa.

Jos esimerkiksi täytyy laskea 2.46³ , niin asetetaan juoksijan hiusviiva X-asteikon (sama asteikko kuin D-asteikko) lukemaan 2.46 ja luetaan vastaus X³-asteikolta. Tulos on arviolta 14.88. Laskimen avulla saatu tarkka vastaus on 14.886936 eli suhteellinen virhe on likimain 0.05 %.

Kuva 12. Laskutoimitus  laskutikun avulla.

Videolinkki (laskutoimitus  laskutikun avulla): https://youtu.be/qa4S5vIYlHo

Kuutiojuuri saadaan hieman vastaavalla kikkailulla kuin neliöjuurikin. Jos halutaan saada esimerkiksi luvun 1245987 kuutiojuuri, niin aluksi juurrettavaa lukua jaetaan tuhannella niin kauan, kunnes saadaan se muunnettua luvuksi, joka on välillä 1…1000. Nyt siis

Asetetaan juoksijan hiusviiva X³-asteikon lukemaa 1.245987 vastaavalle kohdalle ja luetaan vastaus X-asteikolta. Tulos on likimain 1.077 eli siis

Laskimen avulla saatu tarkka vastaus on

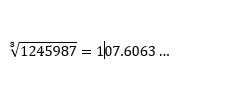
eli suhteellinen virhe on likimain 0.09 %.

Kuva 13. Luvun  kuutiojuuri laskutikun avulla.

Videolinkki (  laskutikun avulla): https://youtu.be/W592KRE0TBM

Johtopäätöksiä ja jatkotutkimuskohteita

Laskutikku on hämmästyttävän tarkka laskentaväline. Esimerkkilaskuissa, joissa käsiteltiin kertolaskua, jakolaskua, toiseen ja kolmanteen potenssiin korottamista ja neliöjuuren ja kuutiojuuren ottoa, päästiin huonoimmillaankin 0.09 % suhteelliseen virheeseen eli parempaan kuin promillen tarkkuuteen. Esimerkiksi rakennustekniikan lujuuslaskelmissa tämä tarkkuus on vielä tänä päivänäkin vähintäänkin riittävä.

Itseltäni puuttuu lähes kokonaan rutiini laskutikun käytössä. Uskon, että harjaantunut laskutikun käyttäjä pystyi aikanaan suoriutumaan monista laskutoimituksista jopa nopeammin kuin nykyaikaisen laskimen käyttäjä. Kokeneen laskutikun käyttäjän arviointitarkkuuskin varmasti on parempi kuin itselläni.

Laskutikun käyttö vaatii äärimmäistä huolellisuutta. Hyvin helposti lukee asteikkoa väärin, jolloin virhe saattaa muodostua suureksikin. Tuloksen suuruusluokan arviointi on asia, johon varmasti harjaantuu, kun laskutikkua enemmän käyttää. Päässälaskutaidosta on myös suuri etu, kun osaa samaan aikaan laskutikun näpelöimisen kanssa päässään arvioida lopputuloksen suuruusluokkaa.

Suurin ongelma kokemukseni mukaan on siinä, että laskutikun käyttäminen vaatii tarkkaa lähinäköä (kuva 14). Minulla oli suuria vaikeuksia saada katsettani tarkennettua niin, että olisin voinut lukea laskutikkua niin tarkasti kuin olisin halunnut ja ehkä myös pystynytkin.

Jatkotutkimuskohteiksi asetin tulevaisuutta ajatellen tehdä tarkempaa analyysia laskutikun laskentatarkkuudesta esimerkiksi kertolaskun ja jakolaskun tapauksessa. Lisäksi aikomus on pureutua laskutikun hyödyntämiseen trigonometristen funktioiden sini, kosini ja tangentti käytössä. Tähän aiheeseen palaan varmasti vielä myöhemmin.

Kuva 14. Traditionaalisen pakollinen laskutikkuselfie. Kuvan henkilö on juuri alkamaisillaan laskutikun tiirailemisen yhdellä silmällä silmälasien ylitse.

Juhani Paananen, lehtori, SeAMK Tekniikka